Bell Shaped Distribution Best Describes the Center of Distribution
For which distribution shape is it usually appropriate to use the median when summarizing the data. The standard deviation measures the ______ of the distribution.
Shape Center And Spread Of A Distribution
It is Bell shaped and symmetrical with the center at u.
. If the distribution is symmetric we will often need to check if it is roughly bell-shaped or has a different shape. Summary of the whole batch of numbers. Explain which measure of central tendency is best to use to represent the center of the distribution based on its skew.
Classifying shapes of distributions. All data that is above the mean. As df gets very large the t distribution gets closer in shape to a normal z-score distribution.
Blitztiger This is an approximately bell-shaped distribution. The fewest scores are at. The normal distribution is a continuous probability distribution that is symmetrical on both sides of the mean so the right side of the center is a mirror image of the left side.
It is rectangular in shape with limits at u-o and uo. Distributions of t are bell-shaped and symmetrical and have a mean of zero. It is Triangular in shape with the peak at u and a base width of 2o.
All data that is between 1 and 3. 2 7 Determining the Mean and Median The Mean. The area under the normal distribution curve represents probability and the total area under the curve sums to one.
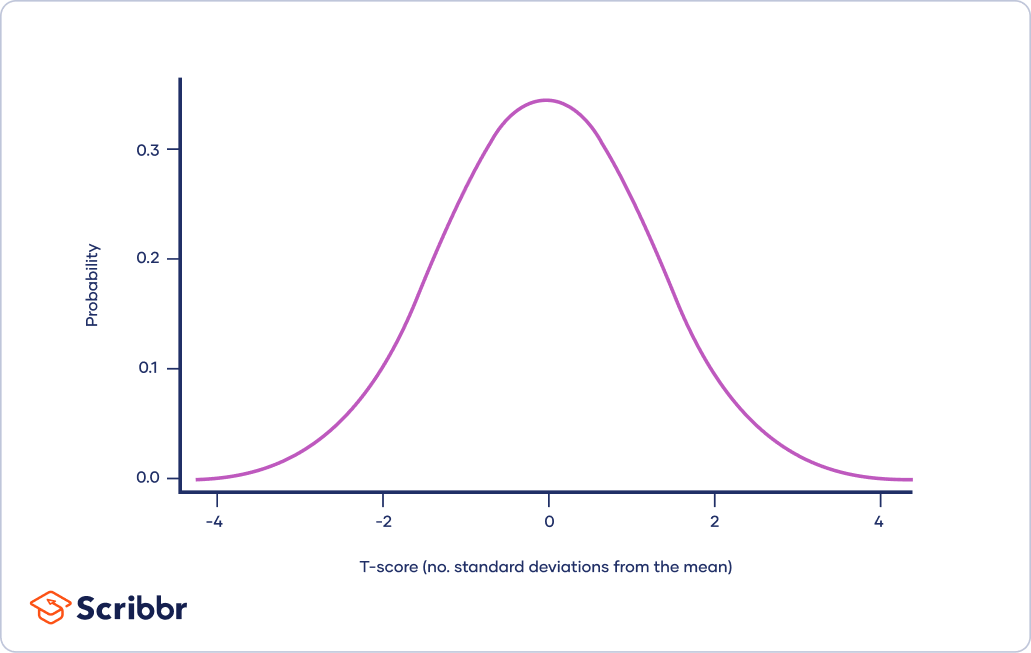
Wikimedia Commons Distributions may also have a single peak or more than one peak. So a bell-shaped curve is a good approximation for the shape of these averages 566 645. The t-distribution tends to be flatter and more spread out whereas the normal z-distribution has more of a central peak.
The highest bar is in the center with height 12. The most common real-life example of this type of distribution is the normal distribution. The exact shape of a t distribution changes with df.
For a distribution that is skewed left which of the following is true. A bell shaped curve is associated with a normal curve. The three common measures of central tendency of a distribution are the arithmetic mean the medianand the mode.
Which best describes the shaded part of this normal distribution graph. The mean is the center of the bell-shaped picture and the standard deviation is the distance from the mean to the inflection point the place where the concavity of the curve changes on the graph. Bell-Shaped A histogram is bell-shaped if it resembles a bell curve and has one single peak in the middle of the distribution.
The mean and standard deviation are not sufficient to describe a distribution that is skewed or has outliers. At a local high school GPAs are normally distributed with a mean of 29 and standard deviation of 06. A typical or representative value.
The two ends are called the tail. In this case the problem says non-symmetric districution which would have to be a skewed distribution. In the case of a distribution where each rectangle is roughly the same height we say we have a uniform distribution.
A normal distribution is projected as a bell shaped distribution with the area can be symmetrically divided into two. Symmetrical distributions that are bell-shaped are also known as normal distributions An example of a normal distribution is pictured below. All data that is one or higher.
Measures of Center. If the highest bar was on the left it would be skewed left and if it was on the right skewed right. Which term best describes the shape of the distribution.
These help describe a distribution too. Describing the distribution of a quantitative variable. For symmetric bell-shaped data the mean and standard deviation provide a good description of the center and shape of the distribution.
This type of distribution has unequal areas of each side which can be left or right. Uniform A histogram is described as uniform if every value in a dataset occurs roughly the same number of times. Just to its left and right are bars of heights 6 and 5.
Mean Median Mode. Use the mean and the median to describe the distribution of relative skill of your team. Is it left right or bell-shaped.
Classifying shapes of distributions. Most of the continuous data values in a normal distribution tend to cluster. How would you describe the shape of the Normal Distribution.
Think of a distribution in terms of an histogram with many bars. All data that is one or more standard deviations above the mean. Two extremes describe spread over 100 of data Range 150 55 95 mph.
This is the currently selected item. In a normal curve most scores obtain scores surrounding the average. The below graphic gives a few examples of the aforementioned distribution shapes.
Center shape and spread are terms used to describe the visual representation of data distribution. Classifying distributions as being symmetric left skewed right skewed uniform or bimodal. Google Classroom Facebook Twitter.
The standard deviation is used in conjunction with the ______ to numerically describe distributions that are bell shaped. A large sample from a normal distribution would describe a bell shaped curve that is symmetrical. Clusters gaps peaks outliers.
Describing the distribution of a quantitative variable. For a normal distribution with and 34 of the values lie between 5 and what number. The ______ measures the center of the distribution.
Explore the definitions and examples of. It is Bell shaped with a long tail on the left side. It represents most scores being in the middle of the distribution.
At the extremes are bars of heights 2 and 1.

Normal Distributions Review Article Khan Academy

T Distribution What It Is And How To Use It With Examples

Chapter 7 The Normal Probability Distribution Flashcards Quizlet
Shape Center And Spread Of A Distribution
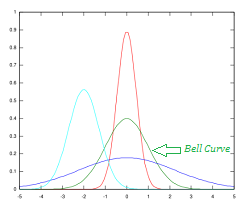
Shapes Of Distributions Definitions Examples Statistics How To
Describing The Shape Of Distributions
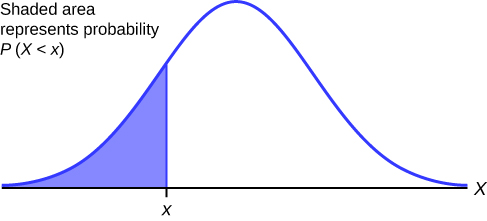
Using The Normal Distribution Introductory Statistics
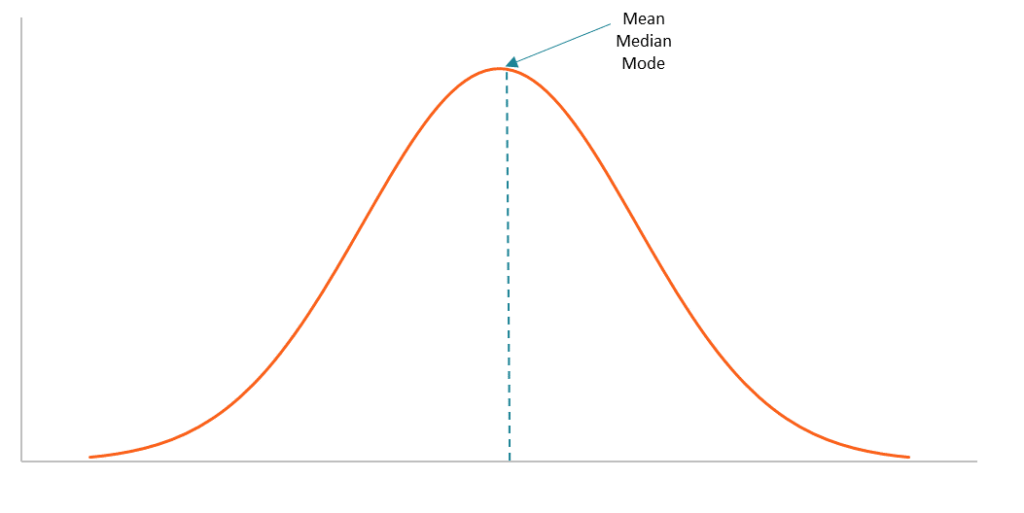
Bell Curve Overview Characteristics And Uses In Finance
/LognormalandNormalDistribution1-7ffee664ca9444a4b2c85c2eac982a0d.png)
Symmetrical Distribution Definition
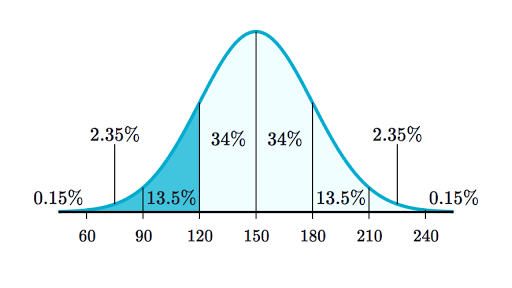
Normal Distributions Review Article Khan Academy
:max_bytes(150000):strip_icc()/LognormalandNormalDistribution1-7ffee664ca9444a4b2c85c2eac982a0d.png)
Symmetrical Distribution Definition
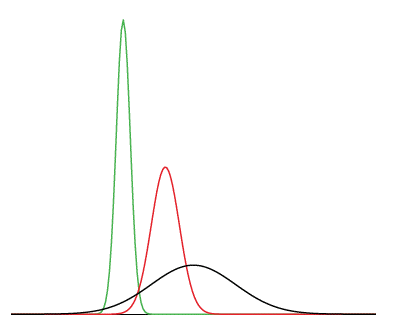
Introduction To Normal Distributions
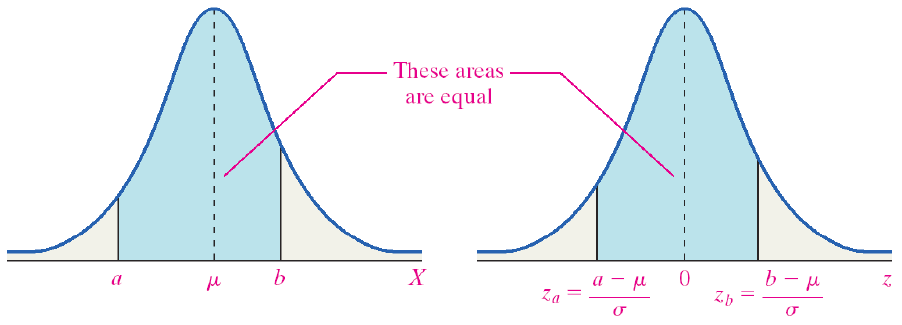
Chapter 1 Descriptive Statistics And The Normal Distribution Natural Resources Biometrics


/dotdash_Final_T_Distribution_Definition_Oct_2020-01-fdfa54d385de4cfca5957da94bbab89f.jpg)



Comments
Post a Comment